Previously, I described a proposed system that will both sign and encrypt code updates using an RSA private key. The goal is to derive the corresponding public key even though it is kept securely within the device.

If you delve into the details of RSA, the public key is the exponent and modulus pair (e, n) and private key is (d, n). The modulus is shared between the two keys and e is almost always 3, 17, or 65537. So in the vendor’s system, only d and n are actually secrets. If we could figure out d, we’ve broken RSA, so that’s likely a dead-end. But if we figure out e and n, we can decrypt the updates.

Let’s see how to efficiently figure out n using guesses of e and a pair of encrypted updates. The signature verification process, RSA-Verify, can be represented by the standard equation shown below in various forms.

The first step is the standard RSA-Pub-Op and the result is m, the padded hash of the message. The remaining steps in RSA-Verify (i.e., validating the signature) are not relevant to this attack. In the second equation, m is refactored to the left side. Finally, 0 mod n is described in an alternate form as k * n. The particular k value is the number of times the odometer has wrapped during exponentiation. It’s not important to us, just the modulus n.

Now, assume we’ve seen two updates and their signatures, sig1 and sig2. We can convert them to the above form by raising each signature to a guess for e and subtracting the associated message m. Note that m is still encrypted and we don’t know its contents.

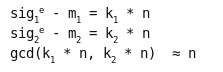
This gives us two values with n as the common factor. The GCD algorithm gives us the common factors of two values very quickly. The reason there is no “=” sign above is that we actually get n times some small prime factors, not just n. Those can easily be removed by trial division by primes up to 1000 since the real factors of n (p and q) are at least 100-digit numbers. Once we have n, we can take each encrypted message and decrypt it with m^e mod n as usual, giving us the plaintext code updates.

I implemented this attack in python for small values of e. Try it out and let me know what you think.

Doing this attack with e = 65537 is difficult due to the fact that it would have to work with values millions of bits long. However, it is feasible and was implemented by Jaffe and Kocher in 1997 using an interesting FFT-multiply method. Perhaps they will publish it at some point. Thanks go to them for explaining this attack to me a few years ago.

Finally, I’d like to reiterate what I’ve said before. Public key cryptosystems and RSA in particular are extremely fragile. Do not use them differently than they were designed. Better yet, seek expert review or design assistance when working with any design involving crypto.

RSA is an extremely malleable primitive and can hardly be called “encryption” in the traditional sense of block ciphers. (If you disagree, try to imagine how AES could be vulnerable to full plaintext exposure to anyone who can submit a message and get a return value of “ok” or “decryption incorrect” based only on the first couple bits.) When I am reviewing a system and see the signing operation described as “RSA-encrypt the signature with the private key,” I know I’ll be finding some kind of flaw in that area of the implementation.

The entire PKCS#1 standard exists to add structure to the payload of RSA to eliminate as much malleability as possible. To distinguish the RSA primitive operation from higher-level constructs that use the RSA primitive, I use the following terminology.

RSA-Pub/Priv-Op	Perform an RSA operation using the appropriate key (exponent/modulus): dataexp mod n
RSA-Encrypt	Add random padding and transform with RSA-Pubkey-Op
RSA-Decrypt	Transform with RSA-Privkey-Op and check padding in result
RSA-Sign	Add padding and transform with RSA-Privkey-Op
RSA-Verify	Transform with RSA-Pubkey-Op and check padding in result, hash data, compare with hash in payload and return True if match, else False

With that out of the way, a common need in embedded systems is secure code updates. A good approach is to RSA-Sign the code updates at the manufacturer. The fielded device then loads the update into RAM, performs RSA-Verify to be sure it is valid, checks version and other info, then applies the update to flash.

One vendor was signing their updates, but decided they also wanted privacy for the update contents. Normally, this would involve encrypting the update with AES-CBC before signing. However, they didn’t want to add another key to the secure processor since the design was nearly complete.

The vendor decided that since they already had an RSA public key in the device for signature verification, they would also encrypt the update to that key, using the corresponding private key. The “public” key was never revealed outside their secure processor so it was considered secret.

Let’s call the public/private key pair P1 and S1, respectively. Here’s their new update process:

On receiving the update, the secure processor would do the inverse, verifying the signature and then decrypting the code. (Astute reader: yes, there would be a chaining problem if encrypting more than one RSA block’s worth of data but let’s assume the code update is small.)

What’s wrong? Nothing, if you’re thinking about RSA in terms of conventional crypto. The vendor is encrypting something to a key that is not provided to an attacker. Shouldn’t this be as secure as a secret AES key? Next post, I’ll reveal how the malleability of the RSA primitive allows n to be easily calculated.