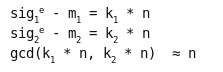(First in a series of articles on attacking hardware and software by inducing faults)
One of the common assumptions software authors make is that the underlying hardware works reliably. Very few operating systems add their own parity bits or CRC to memory accesses. Even fewer applications check the results of a computation. Yet when it comes to cryptography and software protection, the attacker controls the platform in some manner and thus faulty operation has to be considered.
Fault induction is often used to test hardware during production or simulation runs. It was probably first observed when mildly radioactive material that is a natural part of chip packaging led to random memory bit flips.
When informed that an attacker in possession of a device can induce faults, most engineers respond that nothing useful could come of that. This is a similar response to when buffer overflows were first discovered in software (“so what, the software crashes?”) I often find this “engineering mentality” gets in the way of improving security, even insisting you must prove exploitability before fixing a problem.
A good overview paper is “The Sorcerer’s Apprentice Guide to Fault Attacks” by Bar-el et al. In their 1997 paper “Low Cost Attacks on Tamper Resistant Devices,” Anderson and Kuhn conclude:
“We have improved on Differential Fault Analysis. Rather than needing about 200 faulty ciphertexts to recover a DES key, we need between one and ten. We can factor RSA moduli with a single faulty ciphertext. We can also reverse engineer completely unknown algorithms; this appears to be faster than Biham and Shamir’s approach in the case of DES, and is particularly easy with algorithms that have a compact software implementation such as RC5.”
This is quite a powerful class of attacks, and is sometimes applicable to software-only systems as well. For instance, a signal handler often can be triggered from remote, inducing faults in execution if the programmer wasn’t careful.
Of course, glitch attacks are most applicable to smart cards, HSMs, and other tamper-resistant hardware. Given the movement to DRM and trusted computing, we can expect to see this category of attack and its defenses become more sophisticated. Why rob banks? Because that’s where the money is.